A. Barisan dan Deret
Kalian tentu pernah berpikir tentang nomor rumah di sisi kiri jalan yang
bernomor ganjil 1, 3, 5, 7, dan seterusnya, sedangkan nomor rumah di
sisi kanan jalan bernomor genap 2, 4, 6, 8, dan seterusnya. Mungkin juga
kalian pernah berpikir dari mana para pakar menyatakan bahwa 10 tahun
ke depan penduduk Indonesia akan menjadi x juta jiwa.
1. Barisan Bilangan
Misalkan seorang anak diberi uang saku orang tuanya setiap minggu
Rp10.000,00. Jika setiap minggu uang sakunya bertambah Rp500,00 maka
dapat dituliskan uang saku dari minggu ke minggu berikutnya adalah
Rp10.000,00, Rp10.500,00, Rp11.000,00, Rp11.500,00, ....
Susunan bilangan-bilangan yang sesuai dengan contoh di atas adalah :
Perhatikan bahwa dari bilangan-bilangan yang disusun berbentuk 10.000,
10.500, 11.000, 11.500, ... mempunyai keteraturan dari urutan pertama,
kedua, ketiga, keempat, dan seterusnya, yaitu bilangan berikutnya
diperoleh dari bilangan sebelumnya ditambah 500. Bilangan-bilangan yang
disusun urut dengan aturan tertentu seperti itulah dikenal dengan nama
barisan bilangan.
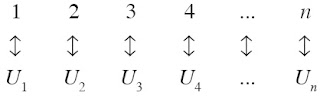
Secara matematis, barisan bilangan merupakan nilai fungsi dengan daerah
definisinya adalah bilangan asli. Misalkan barisan bilangan ditulis
lambang U untuk menyatakan urutan suku-sukunya maka bilangan pertama
ditulis U(1) atau U1, bilangan kedua ditulis U(2) atau U2, dan seterusnya. Jika kita buat korespondensi, akan terlihat seperti berikut.
Jadi, bentuk umum barisan bilangan adalah U1, U2,
U3, ..., Un, ...
Dalam hal ini, Un = f(n) disebut rumus umum suku ke-n dari barisan bilangan.
Contoh Soal Barisan Bilangan 1 :
Diketahui barisan bilangan dengan suku ke-n berbentuk Un = n2 – 2n. Tuliskan 5 suku pertama dari barisan tersebut.
Pembahasan :
Rumus suku ke-n adalah Un = n2 – 2n.
Suku pertama dapat dicari dengan menyubstitusikan n = 1 dan diperoleh U1 = 12 – 2(1) = –1. Suku kedua dicari dengan mensubstitusikan n = 2 dan diperoleh U2 = 22 – 2(2) = 0.
Dengan cara yang sama, diperoleh sebagai berikut.
Suku ketiga = U3 = 32 – 2(3) = 3.
Suku keempat = U4 = 42 – 2(4) = 8.
Suku
kelima = U5 = 52 – 2(5) = 15.
Jadi, lima suku pertama dari barisan itu adalah –1, 0, 3, 8, 15.
Misalkan diberikan suatu barisan bilangan dengan suku ke-n dari barisan
bilangan tersebut tidak diketahui. Dapatkah kita menentukan rumus suku
ke-n? Hal ini tidak selalu dapat ditentukan, tetapi pada beberapa
barisan kita dapat melakukannya dengan memperhatikan pola suku-suku
barisan tersebut.
Contoh Soal 2 :
Diketahui barisan bilangan 4, 7, 12, 19, ....
a. Tentukan rumus suku ke-n.
b. Suku keberapa dari barisan tersebut yang bernilai 199?
Penyelesaian :
Barisan bilangan: 4, 7, 12, 19, ...
a. Suku ke-1 = U1 = 4 = 12 + 3
Suku ke-2 = U2 = 7 = 22 + 3
Suku ke-3 = U3 = 12 = 32 + 3
Suku ke-4 = U4 = 19 = 42 + 3
Suku ke-n = Un = n2 + 3
Jadi, rumus suku ke-n barisan tersebut adalah Un = n2 + 3.
b. Diketahui suku ke-n = 199, berarti
Un = 199
↔ n2 + 3 = 199
↔ n2 = 196
Karena n2 = 196 maka n1 = 14 atau n2 = –14 (dipilih nilai n positif).
Mengapa tidak dipilih n = –14?
Jadi, suku yang nilainya 199 adalah suku ke-14.
2. Deret Bilangan
Misalkan kita mempunyai barisan bilangan U1, U2,
U3, ..., Un dan Sn adalah jumlah dari suku-suku barisan itu.
Sn = Sn = U1 + U2 + U3 + ... + Un disebut deret.
Sn = Sn = U1 + U2 + U3 + ... + Un disebut deret.
Jadi, deret adalah jumlahan suku-suku dari suatu barisan.
B. Barisan dan Deret Aritmatika
1. Barisan Aritmatika
Indah menyisihkan sebagaian uang yang dimilikinya untuk disimpan. Pada
bulan ke-1, ia menyimpan Rp 20.000,00. Bulan berikutnya ia selalu
menaikkan simpanannya Rp 500,00 lebih besar dari bulan sebelumnya. Bear
simpanan (dalam rupiah) Indah dari pertama dan seterusnya dapat ditulis
sebagai berikut.
Bulan Ke-1
|
Bulan Ke-2
|
Bulan Ke-3
|
Bulan Ke-4
|
...
|
20.000
|
20.500
|
21.000
|
21.500
|
...
|
Jika kalian amati, selisih suku barisan ke suku berikutnya selalu tetap, yaitu 500.
Barisan aritmetika adalah suatu barisan bilangan yang selisih setiap dua
suku berturutan selalu merupakan bilangan tetap (konstan).
Bilangan yang tetap tersebut disebut beda dan dilambangkan dengan b.
Perhatikan juga barisan-barisan bilangan berikut ini.
a. 1, 4, 7, 10, 13, ...
b. 2, 8, 14, 20, ...
c. 30, 25, 20, 15, ...
Barisan-barisan tersebut merupakan contoh dari barisan aritmatika.
Mari kita tinjau satu per satu.
a. Pada barisan ini, suku berikutnya diperoleh dari suku sebelumnya ditambah 3. Dapat dikatakan bahwa beda sukunya 3 atau b = 3.
b. Pada barisan ini, suku berikutnya diperoleh dari suku sebelumnya ditambah 6. Dapat dikatakan bahwa beda sukunya 6 atau b = 6.
c. Pada barisan ini, suku berikutnya diperoleh dari suku sebelumnya
ditambah –5. Dapat dikatakan bahwa beda sukunya –5 atau b = –5. Secara
umum dapat dikatakan sebagai berikut. Jika Un adalah suku ke-n dari suatu barisan aritmetika maka berlaku b = Un – Un-1.
Rumus umum suku ke-n barisan aritmetika dengan suku pertama (U1)
dilambangkan dengan a dan beda dengan b dapat ditentukan seperti
berikut.
U1 = a
U2 = U1 + b = a + b
U3 = U2 + b = (a + b) + b = a + 2b
U4 = U3 + b = (a + 2b) + b = a + 3b
U5 = U4 + b = (a + 3b) + b = a + 4b
.
.
.
n = Un–1 + b = a + (n – 1)b
Jadi, rumus suku ke-n dari barisan aritmatika adalah :
Un = a + (n –
1)b
Keterangan:
Un = suku ke-n
a = suku pertama
b = beda
n = banyak suku
Contoh Soal Barisan Aritmatika 3 :
Tentukan suku ke-8 dan ke-20 dari barisan –3, 2, 7, 12, ....
Jawaban :
–3, 2, 7, 12, …
Suku pertama adalah a = –3 dan bedanya b = 2 – (–3) = 5.
Dengan menyubstitusikan a dan b, diperoleh Un = –3 + (n – 1)5.
Suku ke-8 : U8 = –3 + (8 – 1)5 = 32.
Suku ke-20 : U20 = –3 + (20 – 1)5 = 92.
Contoh Soal 4 :
Diketahui barisan aritmetika –2, 1, 4, 7, ..., 40. Tentukan banyak suku barisan tersebut.
Penyelesaian :
Diketahui barisan aritmetika –2, 1, 4, 7, ..., 40.
Dari barisan tersebut, diperoleh a = –2, b = 1 – (–2) = 3, dan Un = 40.
Rumus suku ke-n adalah Un = a + (n – 1)b sehingga :
40 = –2 + (n – 1)3
↔ 40 = 3n – 5
↔ 3n = 45
Karena 3n = 45, diperoleh n = 15.
Jadi, banyaknya suku dari barisan di atas adalah 15.
Contoh Soal 5 :
Suku ke-10 dan suku ke-14 dari barisan aritmetika berturut-turut adalah 7
dan 15. Tentukan suku pertama, beda, dan suku ke-20 barisan tersebut.
Pembahasan :
Diketahui U10 = 7 dan U14 = 15. Dari rumus suku ke-n barisan aritmetika Un = a + (n – 1)b, diperoleh 2 persamaan, yaitu :
U10 = 7 sehingga diperoleh a + 9b = 7 ............................ (1)
U14 = 15 sehingga diperoleh a + 13b = 15 ........................ (2)
Untuk menentukan nilai a dan b, kita gunakan metode campuran antara
eliminasi dan substitusi. Dari persamaan (1) dan (2), diperoleh :
a
+
9b
|
= 7
|
|
a
+
13b
|
= 15
|
-
|
–4b
|
= –6
|
|
b
|
= 2
|
Dengan menyubstitusikan b = 2 ke persamaan (1), diperoleh :
a + 9(2) = 7 ↔ a = –11
Dengan demikian, diperoleh suku ke-n adalah Un = –11 + (n – 1)2.
Jadi, suku ke-20 adalah U20 = –11 + (20 – 1)2 = 27.
Pola Kuadrat dari Bilangan 9
Apakah hasil kuadrat bilangan yang disusun dari angka 9 memiliki pola
tertentu? Betul sekali. Hasil kuadratnya hanya tersusun dari angka 9, 8,
1, dan 0. Jika bilangan terdiri atas n digit angka 9 (n bilangan bulat
kurang dari 10) maka kuadrat bilangan tersebut adalah bilangan yang
tersusun dari angka 9 sebanyak n – 1, diikuti angka 8, kemudian angka 0
sebanyak n – 1, dan diakhiri angka 1. Perhatikan pola berikut.
92 = 81
992 = 9801
9992 = 998001
99992 = 99980001
999992 = 9999800001
9999992 = 999998000001
Setelah memperhatikan pola di atas, coba kalian tentukan hasil dari :
a. 99999992
b. 999999992
c.
9999999992
2. Deret Aritmetika
Dari sembarang barisan aritmetika, misalnya 2, 5, 8, 11, 14, ... dapat
dibentuk suatu deret yang merupakan penjumlahan berurut dari suku-suku
barisan tersebut, yaitu 2 + 5 + 8 + 11 + .... Terlihat bahwa barisan
aritmetika dapat dibentuk menjadi deret aritmetika dengan cara
menjumlahkan suku-suku barisan aritmetika sehingga dapat didefinisikan
secara umum.
Misalkan U1, U2,
U3, ..., Un merupakan suku-suku dari suatu barisan aritmetika. U1 + U2
+ U3 + ... + Un disebut deret aritmetika, dengan :
Un = a + (n – 1)b.
Seperti telah kalian ketahui, deret aritmetika adalah jumlah n suku
pertama barisan aritmetika. Jumlah n suku pertama dari suatu barisan
bilangan dinotasikan Sn. Dengan demikian,
Sn = U1
+ U2 + U3 + ... + Un.
Untuk memahami langkah-langkah menentukan rumus Sn, perhatikan contoh berikut.
Contoh Soal Deret Aritmatika 6 :
Diketahui suatu barisan aritmetika 2, 5, 8, 11, 14. Tentukan jumlah kelima suku barisan tersebut.
Pembahasan :
Jumlah kelima suku 2, 5, 8, 11, 14 dapat dituliskan sebagai berikut.
S5 =
|
2 + 5 + 8 + 11
+ 14
|
|
S5 =
|
14 + 11 + 8 +
5 + 2
|
+
|
2S5 =
|
16 + 16 + 16 +
16 + 16
|
|
2S5 =
|
5 x 16
|
|
S5 =
|
Jadi, jumlah kelima suku barisan tersebut adalah 40.
Setelah kalian amati contoh di atas, kita dapat menentukan rumus umum untuk Sn sebagai berikut.
Diketahui rumus umum suku ke-n dari barisan aritmetika adalah Un = a + (n – 1)b. Oleh karena itu,
U1
=
|
a
|
= a
|
||
U2
=
|
a
|
+
|
b
|
= Un – (n – 2)b
|
U3
=
|
a
|
+
|
2b
|
= Un – (n – 3)b
|
.
|
.
|
.
|
||
.
|
.
|
.
|
||
.
|
.
|
.
|
||
Un
=
|
a
|
+
|
(n – 1)b
|
= Un
|
Dengan demikian, diperoleh :
Sn = a + (a + b) + (a + 2b) + ... + (a + (n – 1)b)
= a + (Un – (n – 2) b) + (Un – (n – 3) b) + ... + Un............ (1)
Dapat pula dinyatakan bahwa besar setiap suku adalah b kurang dari suku berikutnya.
Un–1 = Un – b
Un–2 = Un–1 – b = Un – 2b
Un–3
= Un–2 – b = Un – 3b
Demikian seterusnya sehingga Sn dapat dituliskan
Sn = a + (Un – (n – 1)b) + … + (Un – 2b) + (Un – b) + Un ...... (2)
Dengan demikian, 2Sn = n(a + Un)
↔ Sn = ½ n(a + Un)
↔ Sn = ½ n(a + (a + (n – 1)b))
↔ Sn
= ½ n(2a + (n – 1)b)
Jadi, rumus umum jumlah n suku pertama deret aritmetika adalah :
Sn = ½ n(a + Un) atau
Sn
= ½ n [2a + (n – 1)b]
Keterangan:
Sn= jumlah n suku pertama
a = suku pertama
b = beda
Un = suku ke-n
n = banyak suku
Contoh Soal 7 :
Carilah jumlah 100 suku pertama dari deret 2 + 4 + 6 + 8 + ....
Jawaban :
Diketahui bahwa a = 2, b = 4 – 2 = 2, dan n = 100.
S100 = ½ × 100 {2(2) + (100 – 1)2}
= 50 {4 + 198}
= 50 (202)
= 10.100
Jadi, jumlah 100 suku pertama dari deret tersebut adalah 10.100.
Contoh Soal 8 :
Hitunglah jumlah semua bilangan asli kelipatan 3 yang kurang dari 100.
Pembahasan :
Bilangan asli kelipatan 3 yang kurang dari 100 adalah 3, 6, 9, 12, ..., 99 sehingga diperoleh a = 3, b = 3, dan Un = 99.
Terlebih dahulu kita cari n sebagai berikut.
Un = a + (n – 1)b
↔ 99 = 3 + (n – 1)3
↔ 3n = 99
↔ n = 33
Jumlah dari deret tersebut adalah :
Sn = ½ n(a + Un)
S33 = ½ × 33(3 + 99)
= 1.683
Jadi, jumlah bilangan asli kelipatan 3 yang kurang dari 100 adalah 1.683.
Contoh Soal 9 :
Dari suatu deret aritmetika diketahui suku pertamanya 11, bedanya 4, dan
jumlah n suku pertamanya adalah 200. Tentukan banyaknya suku dari deret
tersebut.
Pembahasan :
Diketahui a = 11, b = 4, dan Sn = 200.
Dari rumus umum jumlah n suku pertama, diperoleh :
Sn = ½ n(2a + (n – 1)b)
↔ 200 = ½ n [2(11) + (n – 1)4]
↔ 400 = n(22 + 4n – 4)
↔ 400 = n(4n + 18)
↔ 4n2
+ 18n – 400 = 0
Jika setiap suku dibagi 2, persamaan tersebut menjadi :
2n2 + 9n – 200 = 0
↔ (n – 8)(2n + 25) = 0
↔ n = 8 atau n =  (diambil n positif karena n bilangan asli)
(diambil n positif karena n bilangan asli)
Jadi, banyak suku deret tersebut adalah 8.
Mennntukan Suku ke-n jika Rumus Jumlah n Suku Pertama Diberikan
Misalkan diberikan suku ke-n barisan aritmetika Sn. Rumus suku ke-n dapat ditentukan dengan
Un = Sn
– Sn–1
Selain dengan menggunakan rumus itu, ada cara lain yang sangat efektif. Misalkan jumlah n suku pertama deret aritmetika adalah :
Sn = pn2 + qn.
Suku ke-n dapat ditentukan dengan :
Un = 2pn + (q – p)
dengan beda 2p.
Contoh Soal 10 :
Jumlah n suku pertama dari deret aritmetika adalah Sn = 2n2 – 4n. Tentukan suku ke-n deret tersebut dan bedanya. Tentukan pula U9.
Penyelesaian :
Sn = 2n2 – 4n → p = 2, q =
–4
Un
= 2pn + (q – p)
= 2 x 2 x n + (–4 – 2)
= 4n – 6
Beda = 2p = 2(2) = 4
Suku ke-10 dapat ditentukan dengan U9 = S9
– S8
S9 = 2(92) – 4(9) = 126
S8 = 2(82) – 4(8) = 96
Jadi, U9 = 126 – 96 = 30
Teorema yang Mengharukan
Apakah kamu tahu teorema yang dikemukakan Pierre de Fermat (1601–1665)? Teorema ini dikembangkan dari teorema Pythagoras yang sangat masyur itu. Menurut teorema Pythagoras, ada banyak pasangan bilangan a, b, dan c yang memenuhi c2 = a2 + b2, seperti 5, 3, dan 4 (beserta kelipatannya); 13, 12, dan 5 (beserta kelipatannya); 25, 24, dan 7 (beserta kelipatannya); dan seterusnya.
Pierre de Fermat mengklaim, tidak ada bilangan bulat a, b, dan c yang memenuhi cn = an + bn, untuk n > 2. Namun, pembuktiannya saat itu masih dipertanyakan. Banyak ilmuwan yang penasaran dengan teorema yang dilontarkan Fermat. Paul Wolfskehl, profesor matematik asal Jerman, awal tahun 1900-an berusaha membuktikan teorema tersebut, namun gagal. Rasa frustasi menyelimutinya, ditambah kekecewaan pada kekasihnya membuat ia berniat bunuh diri. Ketika waktu untuk bunuh diri sudah dekat, ia masih penasaran dan mencoba lagi membuktikan Teorema Fermat membuat dia lupa untuk bunuh diri. Sampai akhir hayatnya, teorema ini belum juga terbuktikan. Wolfskehl berwasiat, ia menyediakan uang 100.000 mark bagi orang pertama yang mampu membuktikan teorema itu. Tahun 1995, Dr. Andrew Wiles, matematikawan dari Universitas Princeton, Inggris, berhasil membuktikan teorema Fermat dengan gemilang. Ia akhirnya mendapat hadiah 200.000 dolar dari Yayasan Raja Faisal di Arab Saudi pada tahun 1997. (Sumber: www.mate-mati-kaku.com)
C. Barisan dan Deret Geometri
Apakah kamu tahu teorema yang dikemukakan Pierre de Fermat (1601–1665)? Teorema ini dikembangkan dari teorema Pythagoras yang sangat masyur itu. Menurut teorema Pythagoras, ada banyak pasangan bilangan a, b, dan c yang memenuhi c2 = a2 + b2, seperti 5, 3, dan 4 (beserta kelipatannya); 13, 12, dan 5 (beserta kelipatannya); 25, 24, dan 7 (beserta kelipatannya); dan seterusnya.
Pierre de Fermat mengklaim, tidak ada bilangan bulat a, b, dan c yang memenuhi cn = an + bn, untuk n > 2. Namun, pembuktiannya saat itu masih dipertanyakan. Banyak ilmuwan yang penasaran dengan teorema yang dilontarkan Fermat. Paul Wolfskehl, profesor matematik asal Jerman, awal tahun 1900-an berusaha membuktikan teorema tersebut, namun gagal. Rasa frustasi menyelimutinya, ditambah kekecewaan pada kekasihnya membuat ia berniat bunuh diri. Ketika waktu untuk bunuh diri sudah dekat, ia masih penasaran dan mencoba lagi membuktikan Teorema Fermat membuat dia lupa untuk bunuh diri. Sampai akhir hayatnya, teorema ini belum juga terbuktikan. Wolfskehl berwasiat, ia menyediakan uang 100.000 mark bagi orang pertama yang mampu membuktikan teorema itu. Tahun 1995, Dr. Andrew Wiles, matematikawan dari Universitas Princeton, Inggris, berhasil membuktikan teorema Fermat dengan gemilang. Ia akhirnya mendapat hadiah 200.000 dolar dari Yayasan Raja Faisal di Arab Saudi pada tahun 1997. (Sumber: www.mate-mati-kaku.com)
C. Barisan dan Deret Geometri
1. Barisan Geometri
Coba kalian amati barisan 1, 2, 4, 8, 16, 32, .... Terlihat, suku
berikutnya diperoleh dengan mengalikan 2 pada suku sebelumnya. Barisan
ini termasuk barisan geometri. Jadi, secara umum, barisan geometri
adalah suatu barisan bilangan yang setiap sukunya diperoleh dari suku
sebelumnya dikalikan dengan suatu bilangan tetap (konstan). Bilangan
yang tetap tersebut dinamakan rasio (pembanding) dan dinotasikan dengan
r.
Perhatikan contoh barisan-barisan berikut.
a. 3, 6, 12, 24, ...
b. 2, 1, ½, 1/4, ...
c. 2, –4, 8, –16, ...
Barisan di atas merupakan contoh barisan geometri. Untuk barisan di atas berturut-turut dapat dihitung rasionya sebagai berikut.
a.  = ..... = 2. Jadi, r = 2.
= ..... = 2. Jadi, r = 2.
b.  = .... Jadi, r = ½
= .... Jadi, r = ½
c.  = –2. Jadi, r = –2.
= –2. Jadi, r = –2.
Dengan demikian, dapat disimpulkan jika U1, U2,
... Un barisan geometri dengan Un adalah rumus ke-n, berlaku :
Rumus umum suku ke-n barisan geometri dengan suku pertama (U1) dinyatakan a dan rasio r, dapat diturunkan sebagai berikut.
U1 =
|
a
|
U2 =
|
U1 × r = ar
|
U3 =
|
U2 × r = ar2
|
U4 =
|
U3 × r = ar3
|
.
|
.
|
.
|
.
|
.
|
.
|
Un =
|
Un–1 × r = arn–2 × r = arn–1
|
Dengan demikian, diperoleh barisan geometri a, ar, ar2, ...,
arn–1, ...
Jadi, rumus umum suku ke-n (Un) barisan geometri adalah :
Un = arn–1
Keterangan:
a = suku pertama
r = rasio
n = banyak suku
Contoh Soal Barisan Geometri 11 :
Carilah suku pertama, rasio, dan suku ke-7 dari barisan geometri berikut.
a. 2, 6, 18, 54, ...
b. 9, –3, 1, -1/3 , ...
Jawaban :
a. 2, 6, 18, 54, ...
Dari barisan geometri di atas, diperoleh :
1) suku pertama: a = 2;
2) rasio: r = ... = ... = 3.
Karena rumus suku ke-n barisan geometri adalah :
Un = arn–1 maka
U7 = 2(37–1) = 2 × 729 = 1.458
b. 9, –3, 1,  , ....
, ....
Dari barisan ini, diperoleh :
1) suku pertama: a = 9;
2) rasio: r =  ;
;
3) suku ke-7: U7 = 
Contoh Soal 12 :
Tiga bilangan membentuk barisan geometri. Jumlah ketiga bilangan itu 21 dan hasil kalinya 216. Tentukan ketiga bilangan itu.
Penyelesaian :
Pemisalan yang mudah untuk barisan geometri adalah  , a, dan ar.
, a, dan ar.
Jumlah ketiga bilangan itu adalah 21 maka  + a + ar = 21.
+ a + ar = 21.
Hasil kali ketiga bilangan adalah 216 maka  × a × ar = 216 ↔ a3 = 216
× a × ar = 216 ↔ a3 = 216
Karena a3 = 216, diperoleh a = 6. Kemudian, substitusikan nilai a = 6 ke persamaan  + a + ar = 21 sehingga diperoleh hasil sebagai berikut.
+ a + ar = 21 sehingga diperoleh hasil sebagai berikut.
↔ 6 + 6r + 6r2 = 21r
↔ 6 – 15r + 6r2 = 0 ........................... (kedua ruas dibagi 3)
↔ 2r2 – 5r + 2 = 0
↔ (2r – 1)(r – 2) = 0
↔ 2r – 1 = 0 atau r – 2 = 0
↔ r = ½ atau r = 2
Dari persamaan di atas, diperoleh r = ½ dan r = 2.
Untuk r = ½ dan a = 6, ketiga bilangan tersebut 12, 6, dan 3.
Untuk r = 2 dan a = 6, ketiga bilangan tersebut 3, 6, dan 12.
Pola Bilangan yang Indah
Perhatikan pola bilangan berikut.
1 × 8 + 1 = 9
12 × 8 + 2 = 98
123 × 8 + 3 = 987
1234 × 8 + 4 = 9876
12345 × 8 + 5 = 98765
123456 × 8 + 6 = 987654
Bandingkan dengan pola bilangan berikut.
0 × 9 + 1 = 1
1 × 9 + 2 = 11
12 × 9 + 3 = 111
123 × 9 + 4 = 1111
1234 × 9 + 5 = 11111
12345 × 9 + 6 = 111111
123456 × 9 + 7 = 1111111
Dari kedua pola bilangan di atas, dapatkah kalian menemukan bentuk umumnya?
Dengan memerhatikan bentuk umum kedua pola bilangan di atas, tentu
kalian dapat dengan mudah menentukan hasil dari pertanyaan berikut.
a. 1234567 × 8 + 7 = ...
b. 12345678 × 8 + 8 = ...
c. 123456789 × 8 + 9 = ...
d. 1234567 × 9 + 8 = ...
e. 12345678 × 9 + 9 = ...
Coba kalian kerjakan.
2. Deret Geometri
Jika U1, U2,
U3, ... Un merupakan barisan geometri maka U1 + U2
+ U3 + ... + Un adalah deret geometri dengan Un = arn–1. Rumus umum untuk menentukan jumlah n suku pertama dari deret geometri dapat diturunkan sebagai berikut.
Misalkan Sn notasi dari jumlah n suku pertama.
Sn = U1 + U2 + ... + Un
Sn
= a + ar + ... + arn–2 + arn–1 .............................................. (1)
Jika kedua ruas dikalikan r, diperoleh :
rSn = ar + ar2 + ar3 + ... + arn–1 + arn ................................... (2)
Dari selisih persamaan (1) dan (2), diperoleh :
rSn =
|
ar + ar2 + ar3 + ... + arn–1 +
arn
|
||
Sn =
|
a
+
|
ar + ar2 + ar3 + ... + arn–1
|
-
|
rSn - Sn =
|
–a + arn
|
||
↔ (r – 1)Sn = a(rn–1)
↔ Sn =
Jadi, rumus umum jumlah n suku pertama dari deret geometri adalah sebagai berikut.
↔ Sn =
Jadi, rumus umum jumlah n suku pertama dari deret geometri adalah sebagai berikut.
Sn =  , untuk r > 1
, untuk r > 1
Sn =  , untuk r < 1
, untuk r < 1
Keterangan:
Sn = jumlah n suku pertama
a = suku pertama
r = rasio
n = banyak suku
Apa yang terjadi jika r bernilai 1?
Contoh Soal Deret Geometri 13 :
Tentukan jumlah dari deret geometri berikut.
a. 2 + 4 + 8 + 16 + ... (8 suku)
b. 12 + 6 + 3 + 1,5 + ... (6 suku)
Pembahasan :
a. 2 + 4 + 8 + 16 + ...
Dari deret tersebut, diperoleh a = 2 dan r = 4/2 = 2 (r > 1).
Jumlah deret sampai 8 suku pertama, berarti n = 8.
Sn =  ↔ S8 =
↔ S8 =  = 2(256 – 1) = 510
= 2(256 – 1) = 510
Jadi, jumlah 8 suku pertama dari deret tersebut adalah 510.
b. 12 + 6 + 3 + 1,5 + ...
Dari deret itu, diperoleh a = 12 dan r =  (r < 1).
(r < 1).
Jumlah deret sampai 6 suku pertama, berarti n = 6.
Sn =  ↔ S6 =
↔ S6 =  = 24(1-
= 24(1-  ) =
) = 
Contoh Soal 14 :
Diketahui deret 3 + 32 + 33
+ ... + 3n = 363. Tentukan :
a. suku pertama;
b. rasio;
c. banyak suku.
c. banyak suku.
Penyelesaian :
Deret 3 + 32 + 33 + ... + 3n = 363
a. Suku pertama: a = 3
b. Rasio: r = ... = .... = 3
c. Untuk Sn = 363
Karena r = 3 > 1, kita gunakan rumus :
Sn = 
↔ 363 = 
↔ 726 = 3n+1 – 3
↔ 3n+1 = 729
↔ 3n+1 = 36
Dengan demikian, diperoleh n + 1 = 6 atau n = 5. Jadi, banyak suku dari deret tersebut adalah 5.
Contoh Soal 15 :
Carilah n terkecil sehingga Sn > 1.000 pada deret geometri 1 + 4 + 16 + 64 + ...
Kunci Jawaban :
Dari deret tersebut, diketahui a = 1 dan r = 4 (r > 1) sehingga jumlah n suku pertamanya dapat ditentukan sebagai berikut.
Sn = 
Nilai n yang mengakibatkan Sn > 1.000 adalah :
Jika kedua ruas dilogaritmakan, diperoleh :
log 4n > log 3.001
↔ n log 4 > log 3.001
↔ n > 
↔ n > 5,78 (Gunakan kalkulator untuk menentukan nilai logaritma)
Jadi, nilai n terkecil agar Sn > 1.000 adalah 6.
Contoh Soal 16 :
Tentukan rumus jumlah n dari deret 1 + 11 + 111 + 1.111 + ...
Penyelesaian :
Jika kalian perhatikan sekilas, deret ini bukan merupakan deret
aritmetika maupun geometri. Namun, coba perhatikan penjabaran berikut.
3. Deret Geometri Tak Berhingga
Deret geometri yang tidak dapat dihitung banyak seluruh sukunya disebut deret geometri tak berhingga.
Perhatikan deret geometri berikut.
a. 1 + 2 + 4 + 8 + ...
c. 1 +  +
+  + ....
+ ....
d. 9 – 3 + 1 –  + .....
+ .....
Deret-deret di atas merupakan contoh deret geometri tak berhingga.
Dari contoh a dan b, rasionya berturut-turut adalah 2 dan –2.
Jika deret tersebut diteruskan maka nilainya akan makin besar dan tidak
terbatas. Deret yang demikian disebut deret divergen, dengan | r | >
1. Sebaliknya, dari contoh c dan d, rasio masing-masing deret 1/2 dan
–1/3. Dari contoh c dan d, dapat kita hitung pendekatan jumlahnya. Deret
tersebut dinamakan deret konvergen dengan | r | < 1. Pada deret
konvergen, jumlah suku-sukunya tidak akan melebihi suatu harga tertentu,
tetapi akan mendekati harga tertentu. Harga tertentu ini disebut jumlah
tak berhingga suku yang dinotasikan dengan S∞ . Nilai S∞ merupakan nilai pendekatan (limit) jumlah seluruh suku (Sn)
dengan n mendekati tak berhingga. Oleh karena itu, rumus deret tak
berhingga dapat diturunkan dari deret geometri dengan suku pertama a,
rasio r dan n → ∞ .
Karena deret konvergen (| r | < 1), untuk n → ∞ maka rn → 0 sehingga :
Jadi, rumus jumlah deret geometri tak berhingga adalah :
Contoh Soal Deret Geometri Tak Terhingga 17 :
Tentukan jumlah tak berhingga suku dari deret berikut.
a. 1 +  +
+  +
+  + ...
+ ...
b. 
Pembahasan :
a. 1 +  +
+  +
+  + ...
+ ...
Dari deret tersebut diketahui a = 1 dan r = ½ sehingga :
b. 
Perhatikan deret 2 + 1 +  +
+  +
+  + ....
+ ....
Dari deret tersebut, diperoleh a = 2 dan r = ½.
Jadi,
Contoh Soal 18 :
Suku pertama suatu deret geometri adalah 2 dan jumlah sampai tak berhingga adalah 4. Carilah rasionya.
Penyelesaian :
Dari soal di atas, unsur-unsur yang diketahui adalah a = 2 dan S∞ = 4.
Kita substitusikan ke dalam rumus S∞ .
S =  ↔ 4 =
↔ 4 = 
↔ 1 – r = ½ .
↔ r = ½
Jadi, rasionya adalah ½.
Contoh Soal 19 :
Sebuah bola jatuh dari ketinggian 10 m dan memantul kembali dengan
ketinggian 3/4 kali tinggi sebelumnya. Pemantulan berlangsung
terus-menerus sehingga bola berhenti. Tentukan jumlah seluruh lintasan
bola. (UMPTN 1995)
Jawaban :
U0 = 10 m; r = 3/4.
U1 = 3/4 x 10 m = 3/40 m
Sn = 10 + 2 S∞ = = 10 + (2 ×  ) = 10 + (2 ×
) = 10 + (2 ×  ) = 10 + (2 × 30) = 70.
) = 10 + (2 × 30) = 70.
Dengan cara lain:
Misalnya suatu benda dijatuhkan dari ketinggian H0 secara
vertikal dan memantul ke atas dengan tinggi pantulan a/b kali dari
ketinggian semula maka panjang lintasan pantulan (H) hingga berhenti
dirumuskan dengan:
Dengan menggunakan cara ini, diketahui a = 3, b = 4, dan H0 = 10 m.
Jadi, H =  = 7 × 10 = 70 m
= 7 × 10 = 70 m



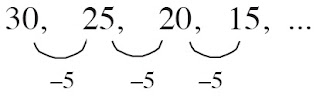
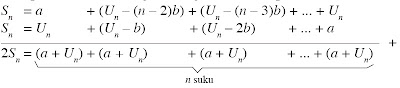
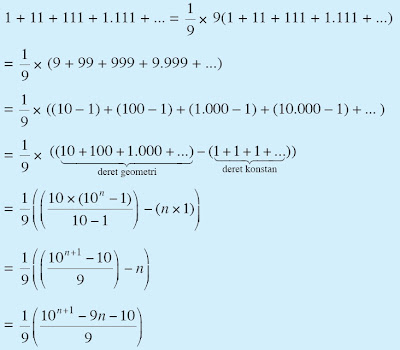
Tidak ada komentar:
Posting Komentar